坐标变换(6)—再谈欧拉角
之前在《坐标变换(2)—不同坐标系下的变换》中简单介绍过欧拉角(Euler,Z-Y-X),如果多加思考,就可能会有下面的问题:用旋转矩阵可以表示旋转或者载体的姿态,那么为何还可以使用欧拉角来表示呢?两者有何联系?接下来让我们逐步分析。
关于欧拉角,网络上的资料非常多,非常杂,容易混淆(比如静态、动态定义),总结起来关于欧拉角的旋转主要分为两类:
- 绕着固定坐标系旋转,某个参考坐标系,例如绕着世界坐标系旋转;
- 绕着载体坐标系的旋转(body frame)。因为载体坐标系固联在载体上,在旋转的过程中,载体坐标系的坐标轴也会跟着旋转;
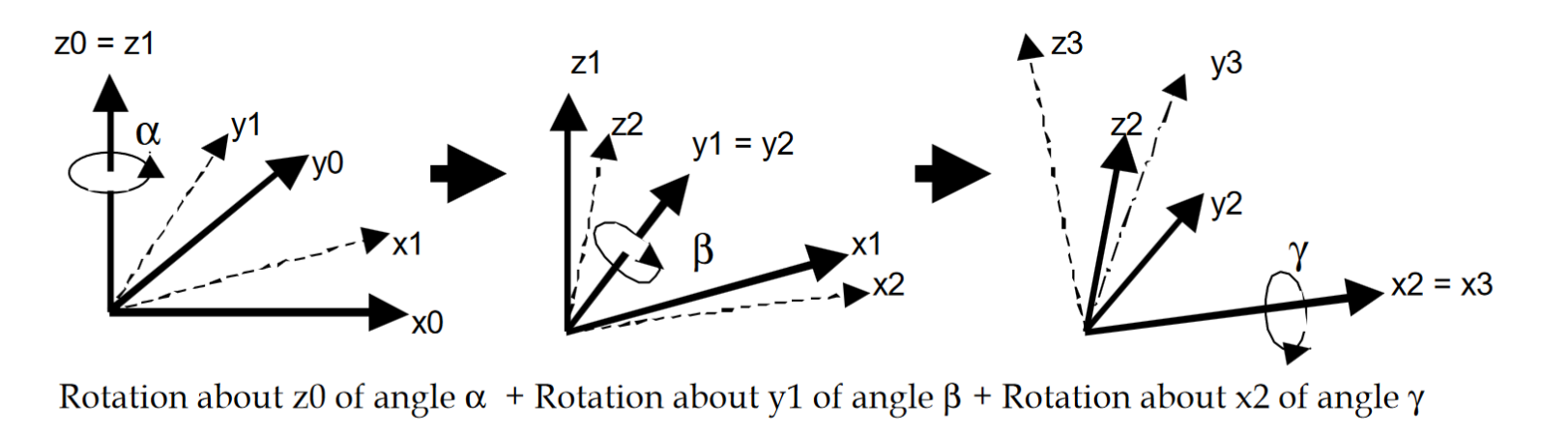
如上图所示,
- 首先绕$z_0$轴旋转$\alpha$角度,此时$x_0y_0z_0$坐标系变成了$x_1y_1z_1$坐标系,其中$z_1$和$z_0$重合,$x_0$和$y_0$都发生了旋转;
- 然后绕着$y_1$,注意不是$y_0$,旋转$\beta$,坐标系变成了$x_2y_2z_2$坐标系。此过程中$y_1$和$y_2$重合,其他两个轴都发生了旋转;
- 最后绕着$x_2$,旋转$\gamma$,$x_0y_0z_0$坐标系变成了$x_3y_3z_3$坐标系。
1.ZYX 欧拉角
上图中,坐标系的旋转过程是围绕载体坐标系body frame进行旋转,旋转的顺序为Z-Y-X(共24种),该定义为ROS中所使用的欧拉角的yaw,pitch,roll的定义,分别为偏航角,俯仰角,横滚角。
There are in total 24 possible xyz arrangements that describe the principal axes frame of a tensor. Correspondingly, there are 24 different sets of Euler angles. Why 24? It's easy to enumerate them: The z axis can point in any of the six principal axis direction of an ellipsoid, and the xy axis pair can have 4 possible orientations for each z orientation, giving 24 in total.
z 轴可以指向椭球体六个主轴方向中的任何一个,而 xy 轴对的每个 z 轴方向可以有 4 个可能的方向,因此总共有 24 个。
这里,
- 假设未旋转之前的坐标系的姿态为初始姿态,此时的载体坐标系$x_0y_0z_0$和世界坐标系的姿态相同,因此$R=I$;
- 因为后续的旋转都是基于载体坐标系为基准进行旋转,在《坐标变换(4)—旋转矩阵》中介绍过,此时每次旋转的旋转矩阵需要进行右乘。
易得,最终旋转的矩阵如下所示,也就是载体坐标系此时在世界坐标系下(参考坐标系)的姿态为$R(\alpha,\beta,\gamma)$,也就是$x_3y_3z_3$坐标系。式中,$c$代码$cos$,而$s$代表$sin$。
$$
\begin{aligned}
R(\alpha,\beta,\gamma)& =IRot(\hat{z},\alpha)Rot(\hat{y},\beta)Rot(\hat{x},\gamma) \\
&\left.=\left(\begin{array}{ccc}c_\alpha c_\beta&c_\alpha s_\beta s_\gamma-s_\alpha c_\gamma&c_\alpha s_\beta c_\gamma+s_\alpha s_\gamma\\s_\alpha c_\beta&s_\alpha s_\beta s_\gamma+c_\alpha c_\gamma&s_\alpha s_\beta c_\gamma-c_\alpha s_\gamma\\-s_\beta&c_\beta s_\gamma&c_\beta c_\gamma\end{array}\right.\right)
\end{aligned}
$$
关于Z-Y-X欧拉角和旋转矩阵的关系后面再详细介绍。
2.XYZ Roll-Pitch-Yaw
欧拉角是基于载体坐标系(body frame),按照一定的顺序绕着坐标轴的旋转。除了绕着载体坐标系,还有一种绕着固定坐标系,例如世界坐标系的旋转,
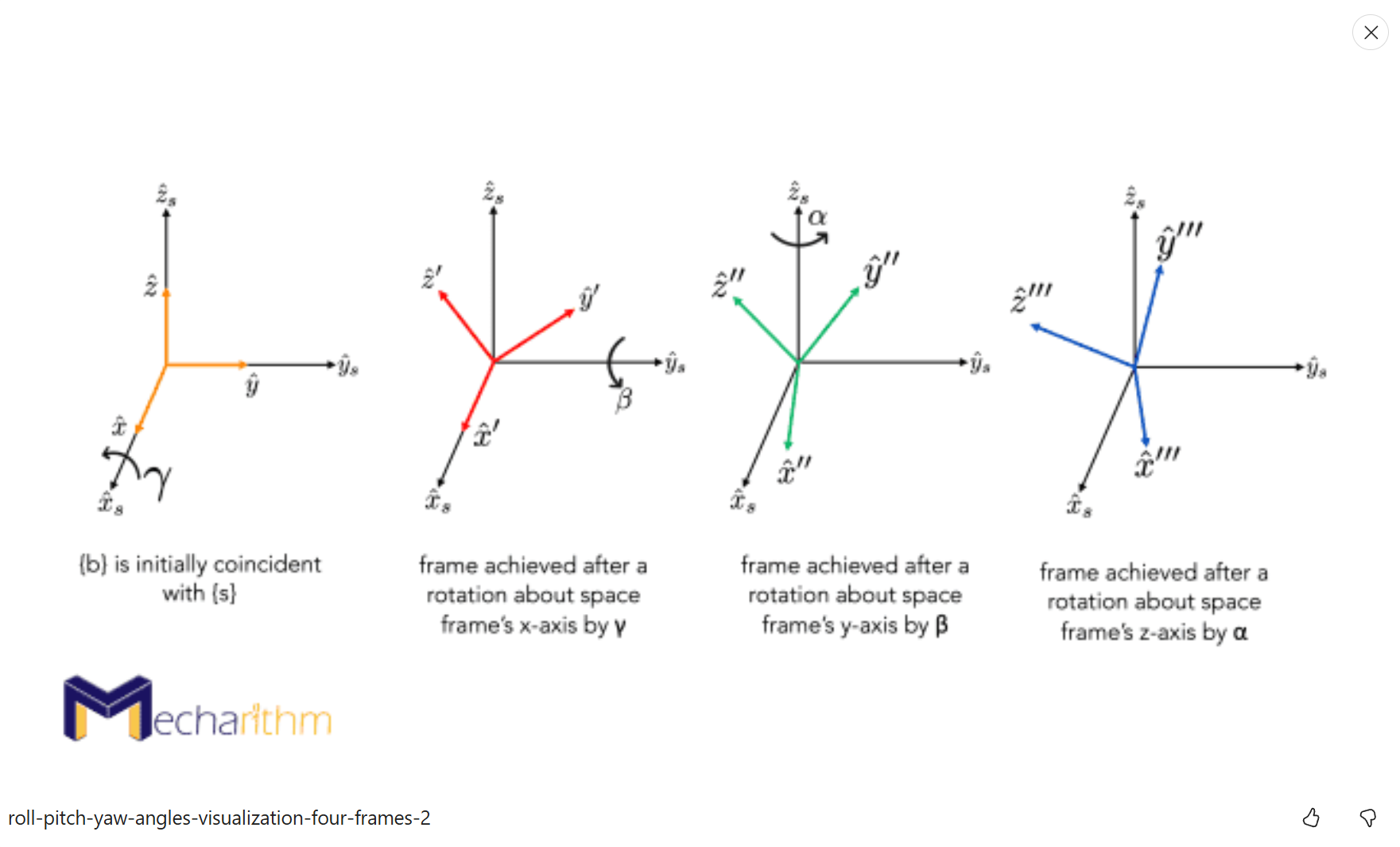
如上图所示,上图中分别绕着参考坐标系中不变的三个坐标轴按照一定的顺序X-Y-Z旋转,
- 首先,绕着参考坐标系的$x$轴旋转$\gamma$;
- 然后,绕着参考坐标系的$y$轴旋转$\beta$;
- 最后,绕着参考坐标系的$z$轴旋转$\alpha$;
这里,
- 假设未旋转之前的坐标系的姿态为初始姿态,此时$R=I$;
- 因为后续的旋转都是基于参考坐标系为基准进行旋转,此时每次旋转的旋转矩阵需要进行左乘。
易得,最终旋转的矩阵如下所示,也就是载体坐标系此时在世界坐标系下(参考坐标系)的姿态为$R(\alpha,\beta,\gamma)$,也就是$x_3y_3z_3$坐标系。式中,$c$代码$cos$,而$s$代表$sin$。
$$
\begin{aligned}
R(\alpha,\beta,\gamma)& =Rot(\hat{z},\alpha)Rot(\hat{y},\beta)Rot(\hat{x},\gamma)I \\
&=\begin{pmatrix}c_\alpha&-s_\alpha&0\\s_\alpha&c_\alpha&0\\0&0&1\end{pmatrix}\begin{pmatrix}c_\beta&0&s_\beta\\0&1&0\\-s_\beta&0&c_\beta\end{pmatrix}\begin{pmatrix}1&0&0\\0&c_\gamma&-s_\gamma\\0&s_\gamma&c_\gamma\end{pmatrix} \\
&=\begin{pmatrix}c_\alpha c_\beta&c_\alpha s_\beta s_\gamma-s_\alpha c_\gamma&c_\alpha s_\beta c_\gamma+s_\alpha s_\gamma\\s_\alpha c_\beta&s_\alpha s_\beta s_\gamma+c_\alpha c_\gamma&s_\alpha s_\beta c_\gamma-c_\alpha s_\gamma\\-s_\beta&c_\beta s_\gamma&c_\beta c_\gamma\end{pmatrix}
\end{aligned}
$$
从结果我们可以看出,此时,X-Y-Z Roll-Pitch-Yaw和Z-Y-X欧拉角的旋转矩阵是相同的,也就是两者具有相同的姿态。
3.从旋转矩阵求欧拉角
我们换一个思路来说明旋转矩阵和欧拉角之间的关系,用欧拉角生成的最终旋转矩阵来求三个欧拉角。
$$
\begin{aligned}&\begin{pmatrix}c_\alpha c_\beta&c_\alpha s_\beta s_\gamma-s_\alpha c_\gamma&c_\alpha s_\beta c_\gamma+s_\alpha s_\gamma\\s_\alpha c_\beta&s_\alpha s_\beta s_\gamma+c_\alpha c_\gamma&s_\alpha s_\beta c_\gamma-c_\alpha s_\gamma\\-s_\beta&c_\beta s_\gamma&c_\beta c_\gamma\end{pmatrix}=\begin{pmatrix}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{pmatrix}\end{aligned}
$$
首先,通过矩阵第一列的前2个元素,我们易得,
$$
cos^2\beta=r_{11}{}^2+r_{21}{}^2\to cos\beta=\pm\sqrt{r_{11}{}^2+r_{21}{}^2}
$$
矩阵第一列的第3个元素,
$$
sin\beta=-r_{31}
$$
当$cos\beta\ne0$,也就是$\beta\ne\pm90°$,此时可以得到,
$$
\begin{array}{l}\beta=atan2(-r_{31},\sqrt{r_{11}{}^2+r_{21}{}^2})\\\text{or}\\\beta=atan2(-r_{31},-\sqrt{r_{11}{}^2+r_{21}{}^2})\end{array}.
$$
对于c语言,上面使用atan2函数而不是atan函数,主要是因为其返回值范围为$[-\pi,\pi]$,对于$tan(α) = sin(α) / cos(α)$,易得下面的结果,
| Quadrant | Angle | sin | cos | tan |
|---|---|---|---|---|
| 第一象限 | $0<\alpha<\pi/2$ | + | + | + |
| 第二象限 | $\pi/2<\alpha<\pi$ | + | - | - |
| 第三象限 | $\pi<\alpha<3\pi/2$ | - | - | + |
| 第四象限 | $3\pi/2<\alpha<2\pi$ | - | + | - |
$tan\alpha$如果是正的,无法区分是第一象限还是第三象限,同理如果是负值,无法区分第二象限还是第四象限。所以atan函数的取值范围为$[-\pi/2,\pi/2]$。
而对于atan2函数,atan2(y, x),which is the projection of a vector with length v and angle α on the y- and x-axis, 因此可以覆盖四个象限。
y = v * sin(α)
x = v * cos(α)当$cos\beta\ne0$,也就是$\beta\ne\pm90°$时,此时,也可以得到$\alpha$和$\gamma$,
$$
\begin{gathered}
\alpha=atan2(\frac{r_{21}}{c_\beta},\frac{r_{11}}{c_\beta}) \\
\gamma=atan2(\frac{r_{32}}{c_\beta},\frac{r_{33}}{c_\beta})
\end{gathered}
$$
4.万向节死锁(gimbal lock)
下面我们处理当$cos\beta=0$时候的情况,此时$\beta=\pm90°$。
当$\beta=90°$时,
$$
\begin{gathered}\begin{pmatrix}0&sin(\gamma-\alpha)&cos(\gamma-\alpha)\\0&cos(\gamma-\alpha)&-sin(\gamma-\alpha)\\-1&0&0\end{pmatrix}=\begin{pmatrix}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{pmatrix} = R_y(\pi/2)R_x(\gamma-\alpha) \end{gathered}
$$
从上述公式我们可以看出,$R_y(\pi/2)R_x(\gamma-\alpha)$,少了绕z轴的旋转,少了一个自由度(gimbal lock),且$r_{31}=-1$,同时,
$$
\begin{array}{l}\gamma-\alpha=atan2(r_{12},r_{22})\\\&\\\gamma-\alpha=atan2(-r_{23},r_{13})\end{array}
$$
此时,$\gamma= \alpha+ atan2(r_{12},r_{22})$。
当$\beta=-90°$时,
$$
\begin{pmatrix}0&-sin(\alpha+\gamma)&-cos(\alpha+\gamma)\\0&cos(\alpha+\gamma)&-sin(\alpha+\gamma)\\1&0&0\end{pmatrix}=\begin{pmatrix}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{pmatrix}
$$
此时,$r_{31}=1$,同时,
$$
\begin{array}{l}\gamma+\alpha=atan2(-r_{12},r_{22})\\\mathrm{or}\\\gamma+\alpha=atan2(-r_{23},-r_{13})\end{array}
$$
此时,$\gamma= -\alpha+ atan2(r_{-23},r_{13})$。
当$\beta=\pm90°$时,是Z-Y-X欧拉角表示法的奇异值点,此时的旋转矩阵可以对应无数的欧拉角,也就是没有唯一解。例如当$\beta=90°$时,假设$\gamma-\alpha$的值是个定值,此时对应的旋转矩阵都是一样的。
例如,下面2个例子,虽然$\alpha$和$\gamma$的值不同,但是两者的差相同,
- 绕Z转60°,绕Y转90°,绕X转10°;
- 绕Z转70°,绕Y转90°,绕X转20°;
通过下面的动画、旋转矩阵的结果(动画中蓝色为Z轴,绿色为Y轴,红色为X轴),我们很容易看到,虽然姿态是一种(旋转矩阵及四元数均相同),但是可以有无数种的欧拉角组合达到该姿态。或者说此时,我们在已知旋转矩阵时是无法得到单一的欧拉角的解。

Z,60°,X,10°,四元数和旋转矩阵,
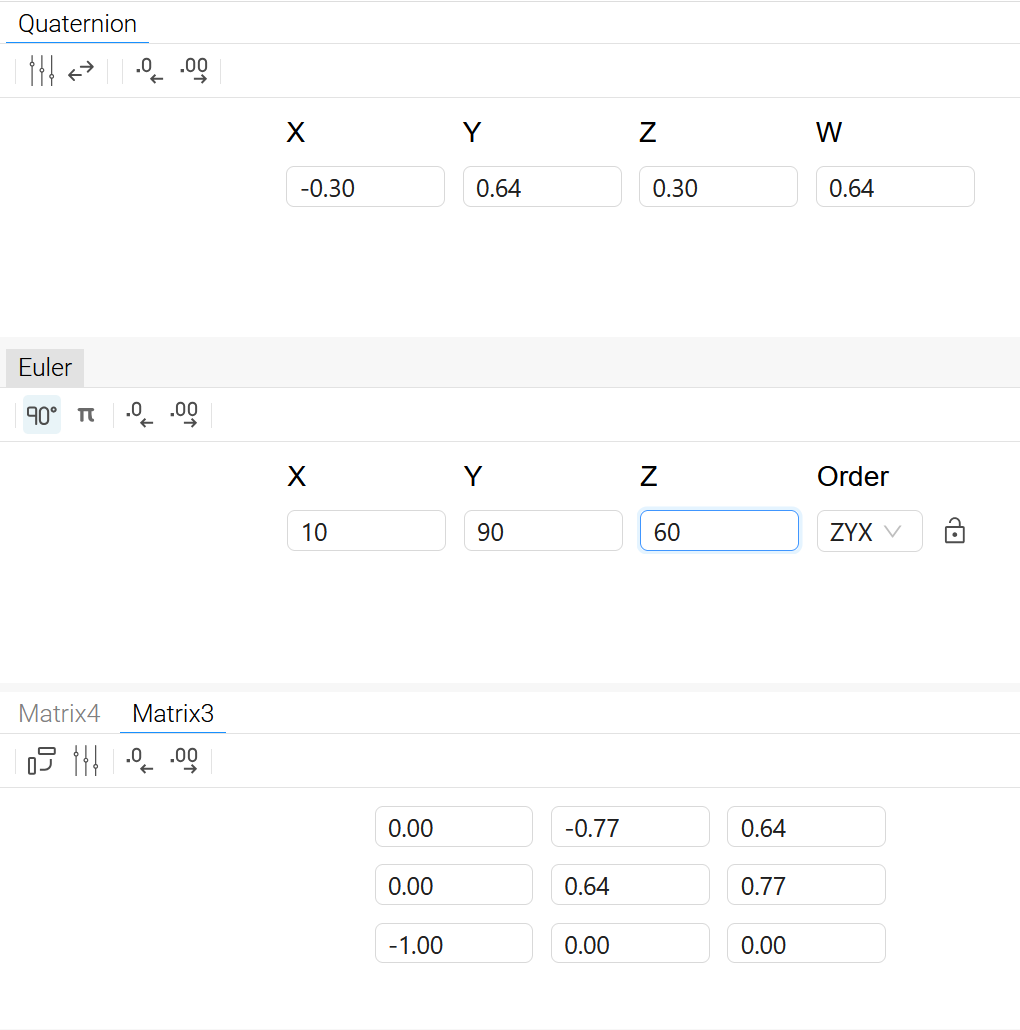
Z,70°,X,20°,四元数和旋转矩阵,
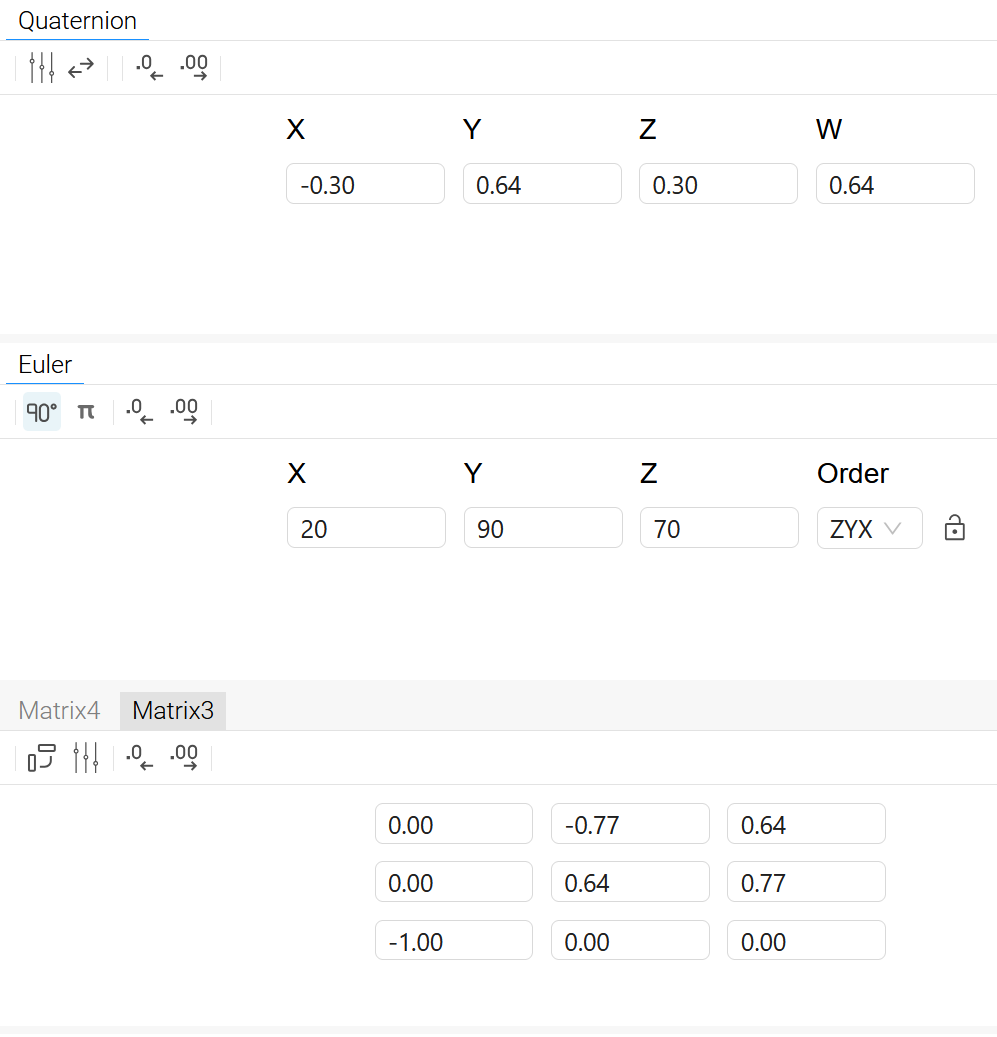
当$\beta=\pm90°$时,此时欧拉角出现奇异值的现象也称为gimbal lock,万向节死锁,为何叫这个名字,如下图所示,每个万向节负责特定轴的旋转,
- 最外层的绿色万向节负责绕着Z轴的旋转,yaw;
- 中间黄色的万向节负责绕着Y轴的旋转,Pitch;
- 最里面的灰色的万向节负责绕着X轴的旋转,Roll;
当绕着Y轴旋转90°时,此时灰色万向节和外层的绿色万向节重合,同轴,像失去了一个万向节一样,所以叫万向节死锁。

关于gimbal lock,我的理解方式:
- 欧拉角是对三个轴按照一定的顺序,例如本文中的Z-Y-X,对载体姿态的进行旋转,载体原始的姿态右乘Z-Y-X对应的旋转矩阵$IRot(\hat{z},\alpha)Rot(\hat{y},\beta)Rot(\hat{x},\gamma)$,在第二步旋转中,如果$\beta=\pm90°$,导致还未旋转的X轴和之前已经旋转过的Z轴重合,进而导致第三步绕X轴的旋转的效果和第一步绕Z轴的旋转效果相同,进而少了一个自由度。
5.ROS中表示旋转的4种方法
- 四元数(quaternion)
- 紧凑的描述;
- 可以无歧义地表示任意方向;
- 计算旋转更加高效,尤其是在插值和级联操作中。
- 但是不直观,难以理解。需要更多的存储空间(4个浮点数)。无法直观地表示物体的角度信息。
- 旋转矩阵(rotation matrix)
- 可以无歧义地表示任意方向。
- 绕着固定轴旋转,roll, pitch, yaw about X, Y, Z axes
- 绕参考坐标系,而不是载体坐标系,例如世界坐标系下的三个轴旋转;
- 主要用于在描述角速度时使用。
- 欧拉角,ros中规定的旋转顺序为Z-Y-X, yaw, pitch, roll
Euler angles are generally discouraged due to having 24 'valid' conventions with different domains using different conventions by default.
- 绕着载体自己的body frame旋转,顺序为Z-Y-X,对应yaw, pitch, roll 。
- 不同的应用领域有不同的旋转次序,注意区分;
- 直观易懂,对人类思维最自然。但是会出现万向节死锁问题。